Gorenstein ring
In commutative algebra, a Gorenstein local ring is a Noetherian commutative local ring R with finite injective dimension, as an R-module. There are many equivalent conditions, some of them listed below, most dealing with some sort of duality condition.
A Gorenstein commutative ring is a commutative ring such that each localization at a prime ideal is a Gorenstein local ring. The Gorenstein ring concept is a special case of the more general Cohen-Macaulay ring.
The classical definition reads:
A local Cohen-Macaulay ring R is called Gorenstein if there is a maximal R-regular sequence in the maximal ideal generating an irreducible ideal.
For a Noetherian commutative local ring 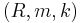 of Krull dimension
of Krull dimension  , the following are equivalent:
, the following are equivalent:
 has finite injective dimension as an
has finite injective dimension as an  -module;
-module; has injective dimension
has injective dimension  as an
as an  -module;
-module;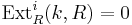 for
for 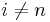 and
and 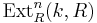 is isomorphic to
is isomorphic to  ;
;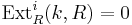 for some
for some 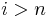 ;
;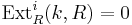 for all
for all 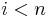 and
and 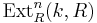 is isomorphic to
is isomorphic to  ;
; is an
is an  -dimensional Gorenstein ring.
-dimensional Gorenstein ring.
A (not necessarily commutative) ring R is called Gorenstein if R has finite injective dimension both as a left R-module and as a right R-module. If R is a local ring, we say R is a local Gorenstein ring.
A noteworthy occurrence of the concept is as one ingredient (among many) of the solution by Andrew Wiles to the Fermat Conjecture.
Examples
- Every local complete intersection ring is Gorenstein.
- Every regular local ring is a complete intersection ring, so is Gorenstein.
- Every field is a regular local ring, so is Gorenstein.
See also
References
- Hideyuki Matsumura, Commutative Ring Theory, Cambridge studies in advanced mathematics 8.